SMAP
Generating High Precision Digital Maps using Circular Arc Splines
Methods for generating High Precision Digital Maps using Circular Arc Splines
Circular Arc Splines and Digital Maps
Arc splines, i.e. curves consisting of circular arcs and straight line segments, provide offset and distance calculations in a closed form and allow a compact representation. Thus, their usage for representing lanes in high precision digital maps has proven its worth in recent research projects (Ko-PER).
SMAP - Minimal Memory Consumption subject to freely selectable Accuracy
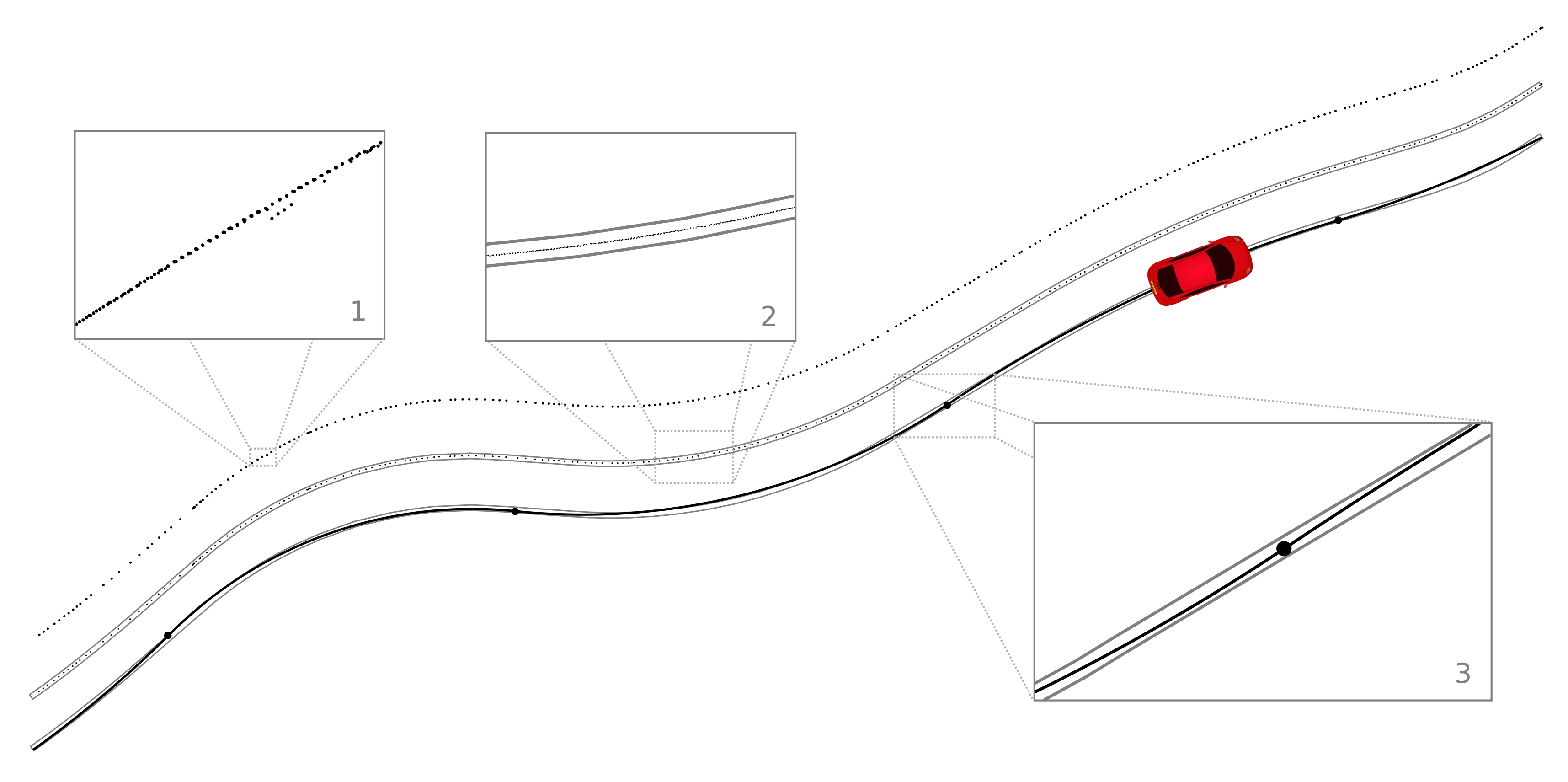
The generation of digital maps usually starts with lane markings given by a point sequence, e.g. extracted from camera images (cf. fig., box 1). However, for a more efficient further processing, individual lanes are required as curves (cf. fig., box 3). These approximating curves should satisfy both high approximation accuracy and compact representation.
The SMAP algorithm, which has been developed at FORWISS (G. Maier, Smooth Minimum Arc Paths), solves this multi-objective optimization problem in an optimal way: Subject to an adjustable maximum deviation from the input points, an arc spline with provably minimal number of arc and line segments (short: segments) is computed. The user defined accuracy is controlled by a so called tolerance channel, which contains a designated start and destination segment (cf. fig., box 2). A Smooth Minimum Arc Path (SMAP) is an arc spline that connects the start segment with the destination segment, runs inside the channel and ensures the minimal number of segmets.
In contrast to various arc spline approximation methods in literature, the breakpoints of the resulting curve are computed automatically and do not have to be chosen from a predefined set of points. This leads to a significant reduction of the resulting number of segments and hence of the memory consumption. The solution is characterized by so called alternating sequences which allow an efficient implementation of the SMAP algorithm. Alternating sequences are families of points on an arc that are alternately touched from the left and from the right by the border of the tolerance channel.
Further Improvements for Map Generation
In order to achieve a fully automated map generation process, cyclic structures, bifurcations and self intersections must be considered. Furthermore the previously described method shall be extended regarding additional smoothing with respect to the mean squared error and further side conditions like for example a restriction of the curvature. Within the DFG-Project “Methods for generating High Precision Digital Maps using Circular Arc Splines“ (http://gepris.dfg.de/gepris/projekt/225923277?language=en) a more general theory of arc spline approximation, which satisfies this challenges, shall be developed.
![]()