HTO
High-Tech-Offensive Bayern: Softwareentwurfssystem für Embedded-PC-Anwendungen
Ziel des Projektes war die Erstellung eines Software-Entwicklungssystems für universelle Automaten. Am Beispiel eines Terminals für das Surfen im Internet wurde verdeutlicht, wie einfach und schnell zukünftige Automaten mit Hilfe der entstandenen Komponenten an Kundenforderungen angepasst und realisiert werden können.
Im Rahmen der High-Tech-Offensive Bayern wurden von FORWISS Passau verschiedene wiederverwendbare parametrierbare Softwarebausteine (Module) im Bereich Bildverarbeitung und optische Messtechnik für das graphische Entwicklungssystem ICONNECT der Firma Micro-Epsilon Messtechnik entwickelt. Über die Möglichkeiten des Demonstrators hinaus können die von FORWISS realisierten Module für Bildverarbeitungsfunktionen in komplexen Fertigungsautomaten verwendet werden.
Im einzelnen wurden folgende Softwarebausteine entwickelt:
- Module zur subpixelgenauen optischen Erfassung von Mustervorlagen
- Module zur Prototyp-Passung
- Module zur Stereobildverarbeitung
- Module zum 3D Matching
- Modul zur Rekonstruktion der räumlichen Lage aufgenommener Kreise
- Module für eine Ebenenrekonstruktion bei bewegtem Messobjekt.
| Subpixelgenaue optische Erfassung von Mustervorlagen |
Eine Reihe von digitalen Bildern (Bild 1, 2, ...) grober Auflösung wird durch Aufnahmen einer Mustervorlage (unten als feinaufgelöstes Musterbild zu sehen), die vor jeder Aufnahme geringfügig versetzt wird, erstellt. Unter Verwendung des entwickelten Rekonstruktionsverfahrens werden die Subpixelbilder (Feinpixelbild 1-3) für verschiedene Rekonstruktionsparameter aus den erhaltenen Grobpixelbildern berechnet. Die im Bild 1, 2 und 3 versteckte Information kann also weitgehend wieder sichtbar gemacht werden.
| Prototyp-Passung |
Unter dem Begriff "Prototyp-Passung" versteht man die automatische Erkennung und Lokalisierung von bekannten Objekten (Prototypen) in digitalen Bildern. Der Prototyp kann dabei als Grauwert-, Farbbild oder durch eine CAD-Vorlage gegeben sein. Das gegebene Objekt kann im digitalen Bild in gedrehter, verschobener und vergrößerter Form auftreten, fallweise auch perspektivisch verzerrt. Außerdem muss mit einer teilweisen Verdeckung des Objekts und Änderungen an der Beleuchtung gerechnet werden.

Für die Bestimmung der Transformation des Prototypen existieren zwei verschiedene Verfahren. Zum einen wird die Position über die Grauwertkorrelation des Prototypbildes ermittelt. Im anderen Fall werden sowohl im Such- als auch im Musterbild markante Bildstrukturen berechnet und einander zugeordnet.
| Stereobildverarbeitung |
Schwerpunkt der Bildverarbeitungsmodule im Bereich Stereo war ohne jegliches Vorwissen aus zwei Bildern einer 3D-Szene soviel Erkenntnis wie möglich zu gewinnen. Wichtigstes Ziel ist hierbei die Ermittlung guter Korrespondenzen (Bildpunkte in den beiden Bildern ein und desselben 3D-Punktes). Daraus kann dann die epipolare Geometrie bestimmt werden. Diese gibt erste Informationen wie die beiden Kameras zueinander orientiert waren. Zudem wird die Korrespondenzfindung auch bei bekannten Kalibrierdaten und Standort der Kameras zueinander ermöglicht.
 |  |
Allein aus diesen zugeordneten Bildpunkten ist schon eine projektive Rekonstruktion, die Geraden und Ebenen erhält, durchführbar. Da für viele Situationen eine Erfassung von Kalibrierdaten und der Standorte der beiden Kameras aufwendig oder gar unmöglich ist (Beispiel: fahrender Roboter mit Kamera), bieten diese Algorithmen Möglichkeiten der Orientierung und Navigation.
| 3D Matching |
Beim 3D Matching wird die geometrische Beziehung zweier Punktewolken zueinander rekonstruiert, d.h. es wird eine Rotation und eine Translation so bestimmt, dass die Punktewolken möglichst genau aufeinanderliegen. Dazu muss aber eine Korrespondenz wenigstens dreier nicht-kollinearer Punkte der ersten Punktwolke zu den entsprechenden Punkten der zweiten Punktwolke bekannt sein.
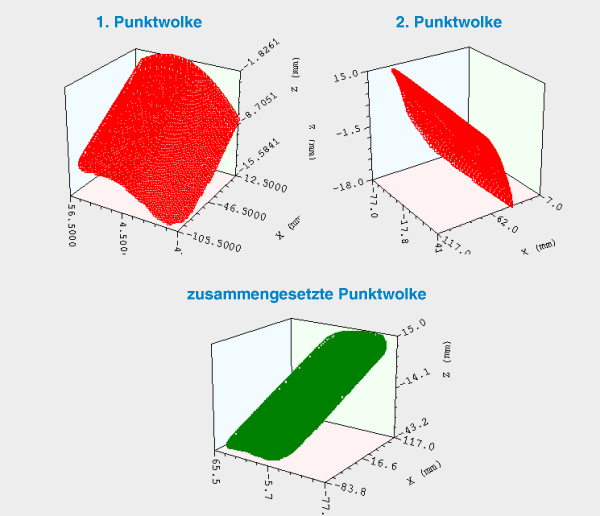
Mit Hilfe dieser Transformation können somit Punktwolken, die beispielsweise von einem 3D Laserscanner stammen zu einer Gesamtpunktmenge mit gleichem Bezugskoordinatensystem vereint werden.
| Rekonstruktion der räumlichen Lage aufgenommener Kreise |
In einigen Anwendungen der Bildverarbeitung ist die Geometrie von aufgenommenen Objekten bereits bekannt. Ist diese Geometrie kreisförmig, z.B. bestimmte Verkehrszeichen oder Markierungen auf Kalibrierplatten, dann ist das aufgenommene Bild im Allgemeinen eine Ellipse. Bestimmt man die Konturpunkte dieser Ellipse dann kann man aus der Lage der Ellipse im Bild und den internen Kameraparametern den Normalenvektor der Ebene bestimmen in der der Kreis liegt. Ist zusätzlich auch noch der Radius des aufgenommenen Kreises bekannt, lässt sich auch der Abstand des Kreises ermitteln. Allerdings gibt es, falls die ermittelte Ellipse nicht bereits ein Kreis ist, immer zwei mögliche Normalenvektoren.
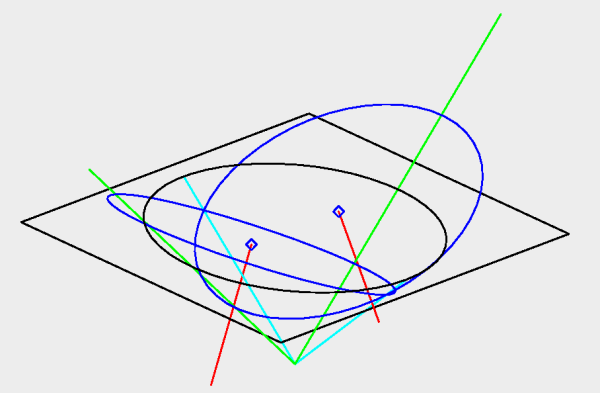
In schwarz eingezeichnet ist eine Ellipse in der Ebene z=1. Strahlen vom Nullpunkt, durch die Ellipse definieren einen elliptischen Kegel, vier dieser Strahlen sind in grün und türkis eingezeichnet. Die zwei blauen Kreise sind in diesem Kegel enthalten. Die Normalen der Ebenen dieser Kreise sind in rot zu sehen.
| Ebenenrekonstruktion bei bewegtem Messobjekt |
Viele Objekte in der menschlichen Umgebung lassen sich mit Ebenen modellieren, z.B. Straßen, Häuser oder die Wände in Räumen. Daher besteht in der Bildverarbeitung häufig das Problem, dass man weiß, dass sich eine Menge von Punkten auf einer Ebene befinden, jedoch nicht die Lage der Ebene. Mit Hilfe der entwickelten Algorithmik ist es möglich, bei Bewegung der Kamera den Normalenvektor der Ebene, in der die Punkte liegen, zu rekonstruieen. Der Abstand der Ebene von der Kamera kann dabei ohne weiteres Nebenwissen nicht ermittelt werden.